about too noisy
what is noise?
noise is a degradation in signal caused by external sources.
in images, noise comes in a few forms. some examples are:
why might we want to reduce image noise
image noise can range from barely visible to so significant that the image is practically all noise
noise reduction can salvage data from such images, and allow useful images to be taken in worse conditions than would otherwise be possible
some examples of areas where noise removal is essential are astronomy, x-ray imaging and ai
how can we reduce image noise
there are many different techniques of reducing noise in images
at tooNoisy, i have implemented 3:
- gaussian blur
- median filter
- bilateral blur
1. gaussian blur
pixel valus are replaced with a weighted average of surrounding pixels
weights are calculated according to the gaussian function
below left is a graph of the one-dimensional gaussian function, and on the right a discrete approximation to a gaussian kernel

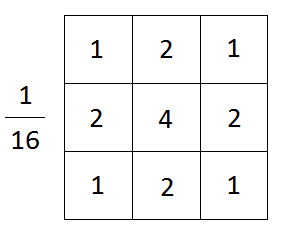
it is a low pass filter often used before edge detection and in low-end digital cameras
and can be applied by convolving with a kernel whose values are taken from the gaussian function
the gaussian blur can be applied as two independant one-dimensional calculations. first, convolve with horizontal kernel, then the vertical one.
this is useful as it means reducing the time complexity of the blur from O(image width * height * kernel width * height) to O(image width * height * kernel width)
in python, gaussian blur can be implemented using numpy (runs quickly as compiled in C)
2. median filter
pixel values are replaced with the medianof surrounding pixels
median of medians algorithm is used to find the median in O(n) time
median filter is best suited to removing salt and pepper noise so is very widely used in digital image processing
it preserves edges demonstrably better
3. bilateral blur
a non-linear, edge preserving and noise-reducing smoothing filter
replaces each pixel with a weighted average of the surrounding pixels
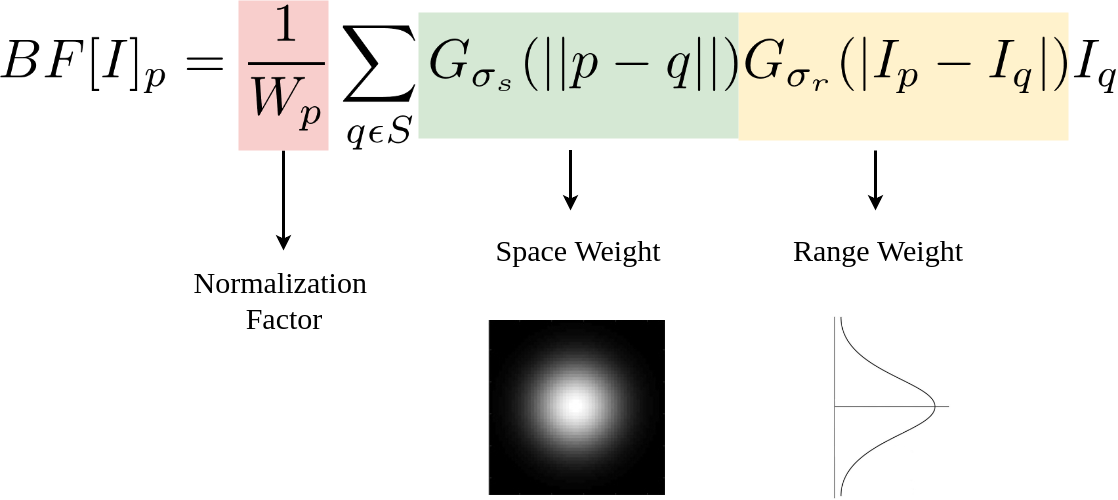
each pixel value is multiplied by two gaussians, one related to distance from the center and one related to intensity.
this has the effect of being much better at preserving edges than the gaussian filter.
the filter is non-linear, and cannot be separated. it is therefor computationally intensive to apply